本栏为本人的LeetCode做题记录，题解均来自LeetCode题解，难懂的地方加入自己的理解。

相关例题

【原题链接】347.前K个高频元素

相关知识博客

暂无

知识点——堆排序

首先介绍堆这种数据结构，堆是一种完全二叉树，分为大顶堆和小顶堆。顾名思义，大顶堆就是所有父结点的值大于等于孩子结点的值组成的树，小顶堆就是所有父结点小于等于孩子结点的值组成的树。
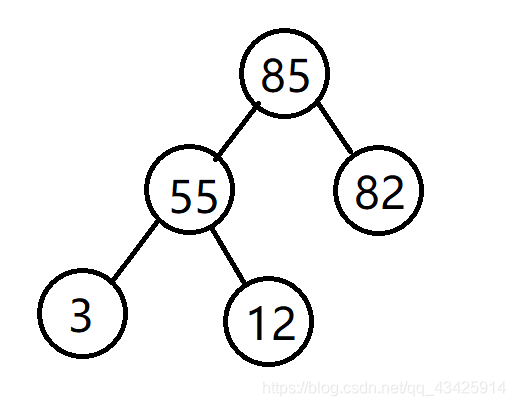
画个图这个概念将非常明确。下图为一个大顶堆，注意堆的以下几个特性：

1. 父节点大于等于子节点
2. 兄弟结点之间的大小无法比较
3. 作为完全二叉树，可以利用数组进行存储。假设下图所示的树层序遍历为[85,55,82,3,12]，此处85起始位置位1。i号位的左孩子下标为2i，右孩子为2i+1。举例：85为1号，2i为2号是55，2i+1为82；55为2号，左孩子为4号位的3，右孩子为5号位的12。

时间复杂度O (nlgn)

调整堆

一开始的时候，可以将任意数组随意地当作完全二叉树，只要我们接下来对它们慢慢调整就可以了。我们选择从上到下进行调整，将当前这个点与孩子结点比较，如果孩子结点中有比自己大的就大方让位和孩子交换位置。接下来继续往下调整，如果比自己的“孙子”之一小，就继续让位，直到自己的值比孩子结点大或者是到达最底层。

理解后就可以写出调整堆的代码了。代码来自《算法笔记》。

参数1：low为当前需要调整的结点的坐标
参数2：high为调整的范围，即往下探底的时候多少是尽头
void downAdjust(int low, int high){
	//i记录需要调整的结点，j为左孩子，可以理解为将要取代父亲的孩子坐标
	//此处先假设是左孩子
	int i = low, j = i*2;
	//如果下标没有越界	
	while(j<=high){
		//如果右孩子没有越界  而且  右孩子比左孩子大则j记录右孩子“篡位”
		//其实此步就是找到左右孩子谁更大记录在j里
		if(j+1<=high && heap[j+1]>heap{j]){
			j = j+1;
		}
		//看看孩子能不能“篡位”，与父节点比
		if(heap[j]>heap[i]){
			//“篡位”成功，交换
			swap(heap[j], heap[i]);
			//待换的结点现在的坐标是j
			i = j;
			//找下一个孩子
			j = i*2;
		}else{
			//不能篡位直接退出
			break;
		}
	}
}

其实调整堆就是整个堆的核心算法，看起来也不难吧。建立堆的过程其实就是把一个乱糟糟的数组经过不断的调整调整成一个有序的堆。那么建堆的代码很快就写出来了。

建堆

建堆的时候唯一的疑问是，不是说每个结点都需要调整吗？其实不用。完全二叉树的性质告诉我们，叶子结点总共有[n/2]个。因此，调整另外一半的非叶子结点就可以了，奥妙就在倒着调整。在倒着调整的过程中，倒数第二层调整结束后，倒数第二层的结点已经完成了与最后一层叶子结点的比较，往上类推，每一层都包含了下一层的信息。

void createHeap(){
	for(int i = n/2 ; i>=1 ;i--){
		downAdjust(i,n);
	}
}

删除堆元素

用最后一个堆元素覆盖堆顶元素，再向下调整即可。

void deleteTop(){
	heap[1] = heap[n--];
	downAdjust(i,n);
}

堆排序的庐山真面目

最后的堆排序代码就像下面这样。这里可能又要问，啊？怎么又变成从n开始所有的倒着遍历一次了？稍微思考一下就得知，创建的是一个大顶堆，最上面的是最大值。那么从最末开始，把最后的元素覆盖与最大值交换，最后排着的不就是最大值了嘛。调整之后不影响堆的结构，然后控制住调整的范围，直到最顶。

void heapSort(){
	createHeap();
	for(int i = n;i>1;i--){
		swap(heap[i],heap[1]);
		downAdjust(1,i-1);
	}
}

其实，优先队列就是使用堆的原理构建的，可以按这个原理创建一个自己的优先队列噢。

题目一347.前K个高频元素

给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

示例 2:
输入: nums = [1], k = 1
输出: [1]

直观的想法是将数组进行排序，再次遍历得到前k高的元素再返回。此处话不多说用维护一个堆的方法来解决这个题。
将这个数组看作是一个完全二叉树。但是我们不需要整个树，只需要树中的前k个结点。后续来的结点要么出现频率高于当前树，否则直接舍弃即可。
原题解来自“瓶子君”。

var buildHeap = (heap,map,k)=>{
    if(k===1)return;
    for(let i = Math.floor(k/2);i>=1;i--){
        heapify(heap,map,k,i);
    }
}
//此处维护一个最小堆
var heapify = (heap , map , k ,i)=>{
    while(true){
        let minIndex = i;
        if(2 * i<=k && map.get(heap[2*i])<map.get(heap[[i]])){
            minIndex = 2*i;
        }
        if(2*i+1 <=k && map.get(heap[2*i+1])<map.get(heap[minIndex])){
            minIndex = 2*i +1;
        }
        if(minIndex!==i){
            swap(heap,i,minIndex);
            i = minIndex;
        }else{
            break;
        }
    }
}
var swap = (arr,i,j)=>{
    let temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}
var topKFrequent = function(nums,k){
    let map = new Map(), heap = [,];
    //map() 方法返回一个新数组
    //数组中的元素为原始数组元素调用函数处理后的值。
    nums.map((num)=>{
        if(map.has(num))map.set(num,map.get(num)+1);
        else map.set(num,1);
    });
    if(map.size<=k){
        return [...map.keys()];
    }
    let i = 0;
    map.forEach((value,key)=>{
        if(i<k){
            heap.push(key);
            if(i===k-1)buildHeap(heap,map,k);
        }else if(map.get(heap[1])<value){//淘汰掉当前最小的，重新维护堆
            heap[1] = key;
            heapify(heap,map,k,1);
        }
        i++;

    })
    heap.shift();//去掉最前面的空
    return heap;
}