本系列索引

• 线性表基础
  • 链表
  • 队列
  • 栈
• 树结构基础
  • 二叉树
  • 堆与优先队列

堆与优先队列定义

在二叉树一文中讲到了完全二叉树，在这里复习一下完全二叉树的概念

完全二叉树是只允许最后一层右侧有空的二叉树，其有如下性质：

1. 编号为 i 的节点(i=1开始)，其左孩子节点编号为 $2\ast i$，其右孩子编号为 $2\ast i+1$
   若 i 从0开始，则其左孩子节点编号为 $2\ast i+1$，其右孩子编号为 $2\ast i+2$
2. 基于第一条性质，完全二叉树可以用数组来表示

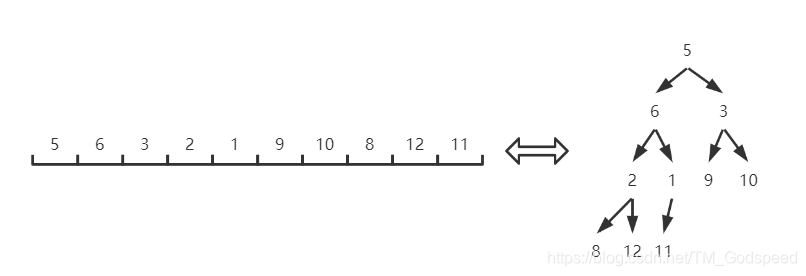
堆 就是通过完全二叉树实现的，通常将堆分为大顶堆和小顶堆

大顶堆

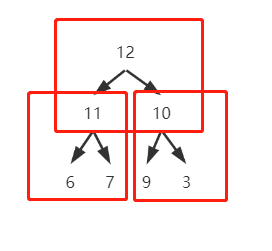
上图为一个简单的大顶堆，其有以下特点：

1. 任意子顶堆的父节点的值比子节点的都大
2. 堆只维护上下关系，也就是说次大值在第二层，第三大值可能在第二层或第三层，第四大值可能在2、3、4层，以此类推；换一个角度来说，只有父子间能比较大小，兄弟间比较不了

小顶堆

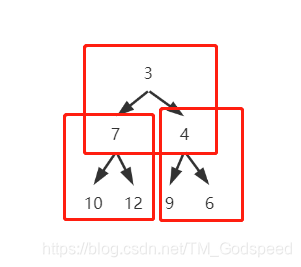
上图为一个简单的小顶堆，性质类比大顶堆

优先队列

回顾一下队列的性质，队列是一种先进先出的数据结构，最常用的是 push 和 pop 两个方法，而堆也有这两个方法。

不同的是，堆 pop() 出来的元素是整个堆元素中的最值，比如大顶堆依次把数据吐出来之后得到的是一个有序的降序序列，因此堆也被称作优先队列，依据此性质我们可以解决和有关维护最值的问题。

堆的实现方式

上文提到过，根据完全二叉树的性质我们可以将堆用数组的方式实现

• pop()
  弹出数组首位元素，将原数组的最后一位进行数组头部的部位，然后进行下沉以维护堆的性质
• push()
  在数组的最后一位推入元素，然后对数组的最后一位进行上浮以维护堆的性质

性质维护

• 上浮
  找到当前节点的父节点并进行比较，以小顶堆举例，如果当前节点的值比父节点的值小，说明要进行交换(如果条件不符合，退出遍历)
• 下沉
  找到当前节点的左右子节点，以小顶堆举例，先标记当前节点，然后和左子节点比较，如果左子节点的值比当前节点小则标记该左子节点，如果右子节点的值比标记点小则标记右子节点，最后交换标记节点和当前节点(如果左右子节点都不符合要求，则退出遍历)

class Heap {
  public heap: number[]
  private readonly kind: boolean
  constructor(arr: number[], kind: 'big' | 'small') {
    this.kind = kind === 'big'
    this.heap = arr

    this.init()
  }

  private init() {
    for (let i = 1; i < this.heap.length; i++) this.sortUp(i)
  }

  size() {
    return this.heap.length
  }

  peek() {
    return this.size() ? this.heap[0] : null
  }

  push(n: number) {
    this.heap.push(n)
    this.sortUp(this.heap.length - 1)
  }

  pop() {
    if (!this.heap.length) return null
    if (this.heap.length === 1) return this.heap.pop()
    const res = this.heap[0]
    this.heap[0] = this.heap.pop()
    this.sortDown(0)
    return res
  }

  private sortUp(index: number) {
    let parentIndex: number
    while (index > 0) {
      parentIndex = (index - 1) >> 1
      if (this.kind) {
        // 大顶堆
        if (this.heap[parentIndex] < this.heap[index]) this.swap(index, parentIndex)
        else break
      } else {
        // 小顶堆
        if (this.heap[parentIndex] > this.heap[index]) this.swap(index, parentIndex)
        else break
      }
      index = parentIndex
    }
  }

  private sortDown(index: number) {
    let leftIndex: number, rightIndex: number, target = index
    while (index < this.heap.length - 1) {
      leftIndex = (index << 1) + 1
      rightIndex = (index << 1) + 2
      if (this.kind) {
        // 大顶堆
        if (leftIndex < this.heap.length && this.heap[leftIndex] > this.heap[target]) target = leftIndex
        if (rightIndex < this.heap.length && this.heap[rightIndex] > this.heap[target]) target = rightIndex
      } else {
        // 小顶堆
        if (leftIndex < this.heap.length && this.heap[leftIndex] < this.heap[target]) target = leftIndex
        if (rightIndex < this.heap.length && this.heap[rightIndex] < this.heap[target]) target = rightIndex
      }
      if (target === index) break
      this.swap(target, index)
      index = target
    }
  }

  private swap(i: number, j: number) {
    [this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]]
  }
}

注意
获取父节点的时候代码使用了位运算，以下三种写法效果等同

parenIndex = (index - 1) >> 1
parenIndex = (index - 1) / 2 | 0
parenIndex = Math.floor((index - 1) / 2)

在初始化的时候，初始化操作是从头开始的，因为如果从尾开始，当遇到当前节点和父节点值相等时，就可能会使堆的性质被破坏

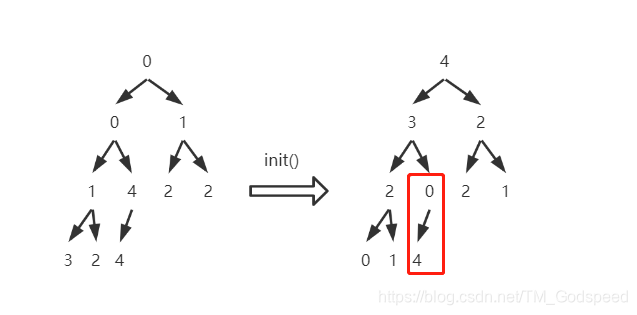
以上代码实现的堆的节点只是一个数字，但是在解决问题的时候，我们通常会使用更加复杂的数据结构，具体见以下习题

习题

在解决以下习题的时候，每次需要用到的堆我都会手动写一遍而不是单纯的复制粘贴。

刚学堆的时候我感觉这是我目前学过最简单的数据结构了，但是实际编写代码的时候出现了不少错误，有很多细节也只有错了之后才发现自己还有那么多细节没有掌握，所以读者希望能掌握这种数据结构的话，建议多写多练

当然有的时候堆并不是题目最优的解决方式，但是本文的习题都会尽量以堆来解决，因为本文的目的是练习堆的使用

leetCode 剑指Offer 40 最小的k个数

看到“最”字，首先想到的就是堆维护最值的性质，所以这道题我们可以建一个小顶堆，前k个弹出的元素就是题目答案

class Heap {
  public heap: number[]
  private readonly kind: boolean
  constructor(arr: number[], kind: 'big' | 'small') {
    this.kind = kind === 'big'
    this.heap = arr
    
    this.init()
  }
  
  private init() {
    for (let i = 1; i < this.heap.length; i++) this.sortUp(i)
  }
  
  push(n: number) {
    this.heap.push(n)
    this.sortUp(this.heap.length - 1)
  }
  
  pop() {
    const res = this.heap.length ? this.heap[0] : null
    this.heap[0] = this.heap.pop()
    this.sortDown(0)
    return res
  }
  
  private sortUp(index: number) {
    let parentIndex: number
    while (index > 0) {
      parentIndex = (index - 1) >> 1
      if (this.kind) {
        // 大顶堆
        if (this.heap[parentIndex] < this.heap[index]) this.swap(index, parentIndex)
        else break
      } else {
        // 小顶堆
        if (this.heap[parentIndex] > this.heap[index]) this.swap(index, parentIndex)
        else break
      }
      index = parentIndex
    }
  }
  
  private sortDown(index: number) {
    let leftIndex: number, rightIndex: number, target = index
    while (index < this.heap.length - 1) {
      leftIndex = (index << 1) + 1
      rightIndex = (index << 1) + 2
      if (this.kind) {
        // 大顶堆
        if (leftIndex < this.heap.length && this.heap[leftIndex] > this.heap[target]) target = leftIndex
        if (rightIndex < this.heap.length && this.heap[rightIndex] > this.heap[target]) target = rightIndex
      } else {
        // 小顶堆
        if (leftIndex < this.heap.length && this.heap[leftIndex] < this.heap[target]) target = leftIndex
        if (rightIndex < this.heap.length && this.heap[rightIndex] < this.heap[target]) target = rightIndex
      }
      if (target === index) break
      this.swap(target, index)
      index = target
    }
  }
  
  private swap(i: number, j: number) {
    [this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]]
  }
}

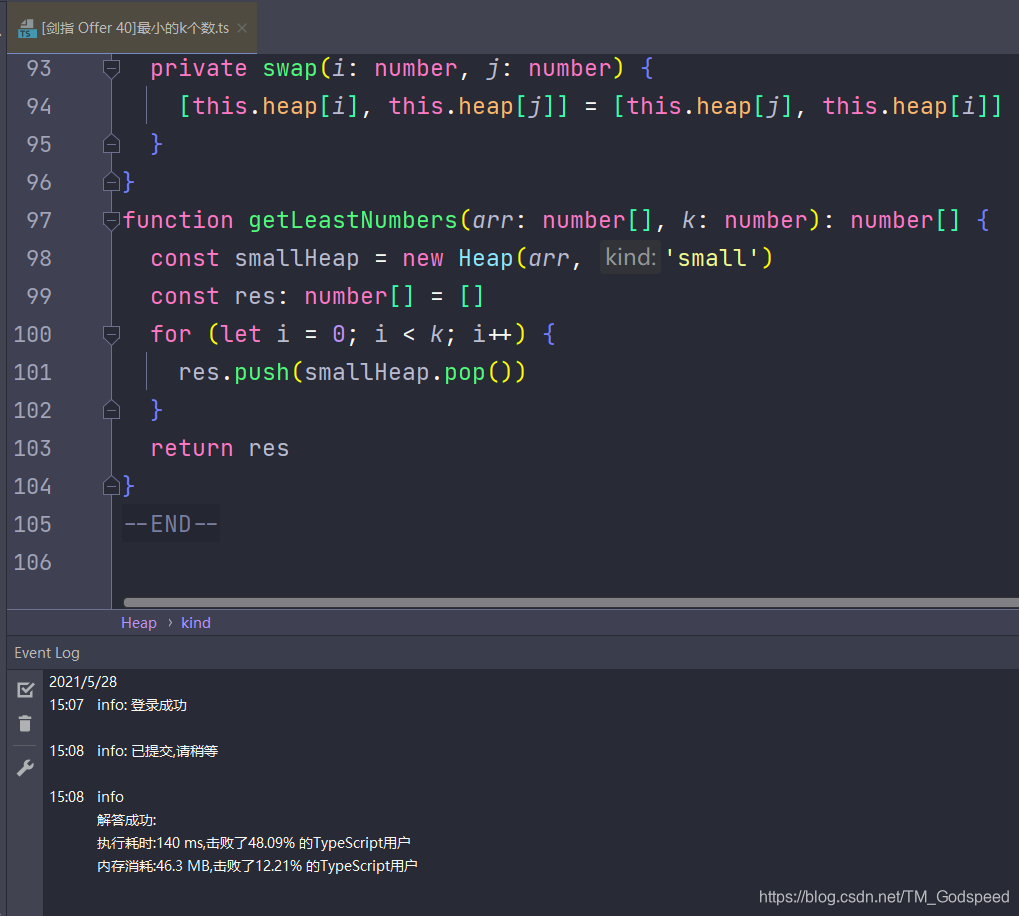
function getLeastNumbers(arr: number[], k: number): number[] {
  const smallHeap = new Heap(arr, 'small')
  const res: number[] = []
  for (let i = 0; i < k; i++) {
    res.push(smallHeap.pop())
  }
  return res
}

leetCode 1046 最后一块石头的重量

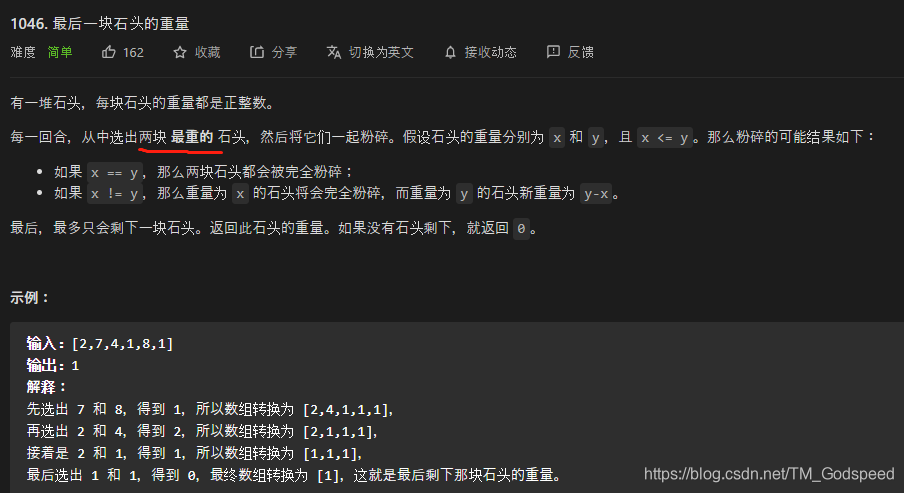
根据题目可知，我们需要一个大顶堆，每次取出两块石头进行操作，最后返回最后一块石头的重量，如果最后没有石头则返回0

class BigHeap {
  public data: number[]
  constructor(data: number[]) {
    this.data = data
    this.init()
  }
  
  init() {
    for (let i = 1; i < this.data.length; i++) this.softUp(i)
  }
  
  size() {
    return this.data.length
  }
  
  push(val: number) {
    this.data.push(val)
    this.softUp(this.data.length - 1)
  }
  
  pop() {
    if (!this.data.length) return null
    if (this.data.length === 1) return this.data.pop()
    const res = this.data[0]
    this.data[0] = this.data.pop()
    this.softDown(0)
    return res
  }
  
  softUp(index: number) {
    let parentIndex: number
    while (index) {
      parentIndex = (index - 1) >> 1
      if (this.data[parentIndex] < this.data[index]) {
        this.swap(index, parentIndex)
        index = parentIndex
      } else break
    }
  }
  
  softDown(index: number) {
    let leftIndex: number, rightIndex: number, target: number
    while (index < this.data.length) {
      leftIndex = (index << 1) + 1
      rightIndex = (index << 1) + 2
      target = index
      if (leftIndex < this.data.length && this.data[leftIndex] > this.data[target]) {
        target = leftIndex
      }
      if (rightIndex < this.data.length && this.data[rightIndex] > this.data[target]) {
        target = rightIndex
      }
      if (index === target) break
      this.swap(index, target)
      index = target
    }
  }
  
  swap(i: number, j: number) {
    [this.data[i], this.data[j]] = [this.data[j], this.data[i]]
  }
}

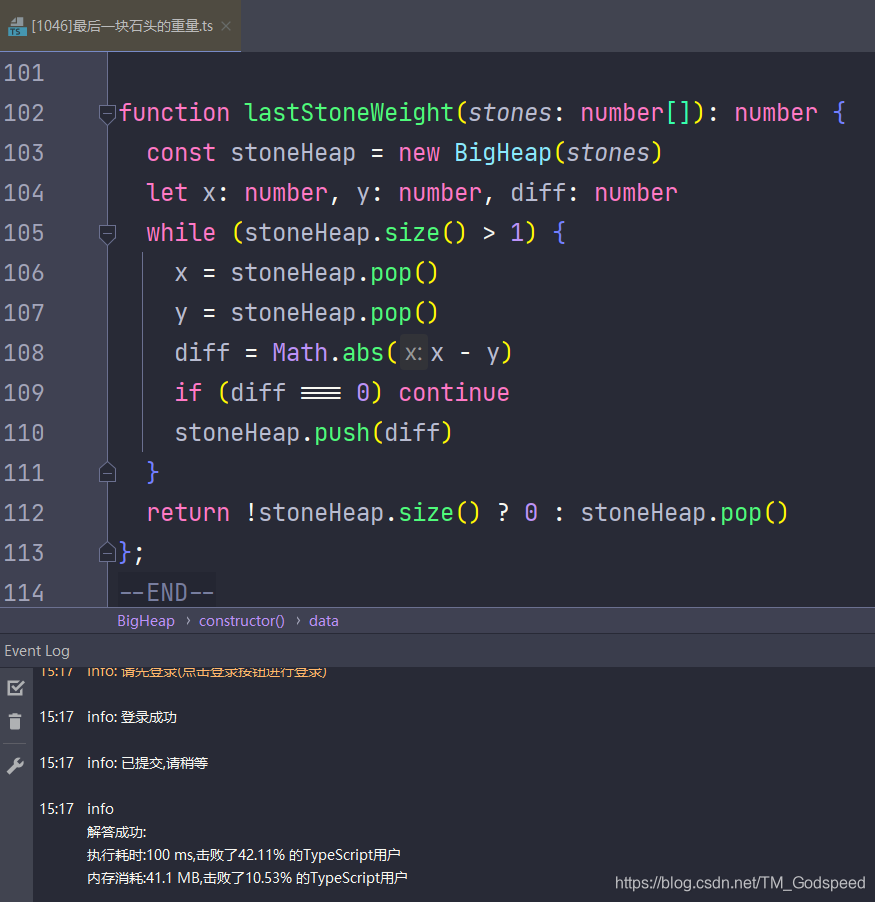
function lastStoneWeight(stones: number[]): number {
  const stoneHeap = new BigHeap(stones)
  let x: number, y: number, diff: number
  while (stoneHeap.size() > 1) {
    x = stoneHeap.pop()
    y = stoneHeap.pop()
    diff = Math.abs(x - y)
    if (diff === 0) continue
    stoneHeap.push(diff)
  }
  return !stoneHeap.size() ? 0 : stoneHeap.pop()
}

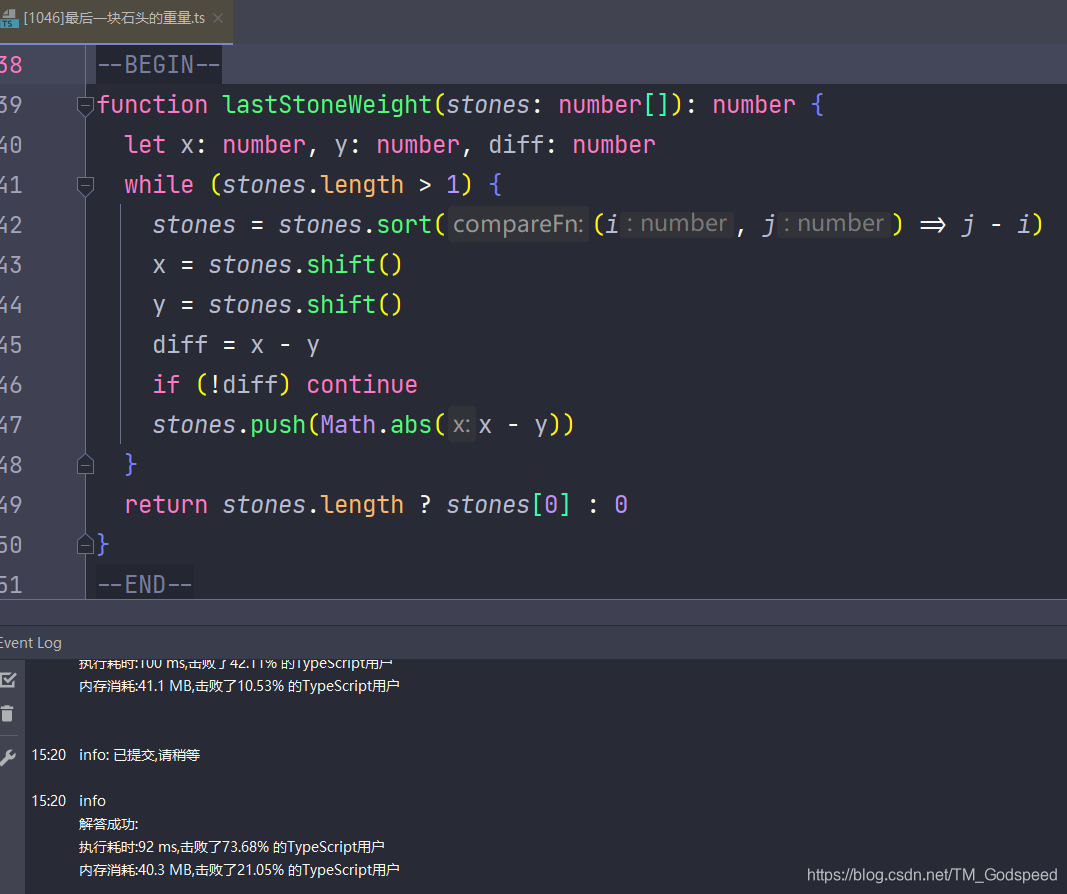
还有一种方法是通过 Array.sort() 对数组进行排序之后取出两个最大的元素进行操作，如此反复直到数组的长度小于2 (只剩一块石头或者没有石头)

function lastStoneWeight(stones: number[]): number {
  let x: number, y: number, diff: number
  while (stones.length > 1) {
    stones = stones.sort((i, j) => j - i)
    x = stones.shift()
    y = stones.shift()
    diff = x - y
    if (!diff) continue
    stones.push(Math.abs(x - y))
  }
  return stones.length ? stones[0] : 0
}

leetCode 703 数据流中的第k大元素

从题目可知，我们可以通过构建一个大顶堆，其吐出来的第k个元素即题目所求

注意这里的元素不能吐出来就丢了，得到结果之后还得让大顶堆吞回去

class BigHeap {
    public data: number[]
    constructor(data: number[]) {
        this.data = data
        this.init()
    }
    
    init() {
        for (let i = 1; i < this.data.length; i++) this.sortUp(i)
    }
    
    peek() {
        return this.data.length ? this.data[0] : null
    }
    
    push(val: number) {
        this.data.push(val)
        this.sortUp(this.data.length - 1)
    }
    
    pop() {
        if (!this.data.length) return null
        if (this.data.length === 1) return this.data.pop()
        const res = this.data[0]
        this.data[0] = this.data.pop()
        this.sortDown(0)
        return res
    }
    
    private sortUp(index: number) {
        let parentIndex: number
        while (index) {
            parentIndex = (index - 1) >> 1
            if (this.data[index] > this.data[parentIndex]) {
                this.swap(index, parentIndex)
                index = parentIndex
            } else break
        }
    }
    
    private sortDown(index: number) {
        let leftIndex: number, rightIndex: number, target: number
        while (index < this.data.length) {
            target = index
            leftIndex = (index << 1) + 1
            rightIndex = (index << 1) + 2
            if (leftIndex < this.data.length && this.data[leftIndex] > this.data[target]) target = leftIndex
            if (rightIndex < this.data.length && this.data[rightIndex] > this.data[target]) target = rightIndex
            if (target === index) break
            this.swap(index, target)
            index = target
        }
    }
    
    private swap(i: number, j: number) {
        [this.data[i], this.data[j]] = [this.data[j], this.data[i]]
    }
}

class KthLargest {
    private nums: BigHeap
    private readonly k: number
    constructor(k: number, nums: number[]) {
        this.nums = new BigHeap(nums)
        this.k = k
    }

    add(val: number): number {
        const temp: number[] = []
        this.nums.push(val)
        for (let i = 0; i < this.k - 1; i++) {
            temp.push(this.nums.pop())
        }
        const res = this.nums.peek()
        const data = this.nums.data
        this.nums = new BigHeap([...temp, ...data])
        return res
    }
}

这道题通过堆去做的话在提交的时候有一个测试用例没有通过，提示运行时间超出限制，这个也是堆的一个弊端，数据量一大的话处理起来就会特别费劲

在经过多次尝试后我依然没有找到优化方法以通过提交测试用例，所以这道题用堆的题解先写到这，大神们可以在评论区给出更优的解法

另外一种方法也是利用 Array.sort()，先让数组排好序再直接取

class KthLargest {
  private nums: number[]
  private readonly k: number
  constructor(k: number, nums: number[]) {
    this.nums = nums
    this.k = k
  }

  add(val: number): number {
    this.nums.push(val)
    this.nums = this.nums.sort((i, j) => j - i)
    return this.nums[this.k - 1]
  }
}

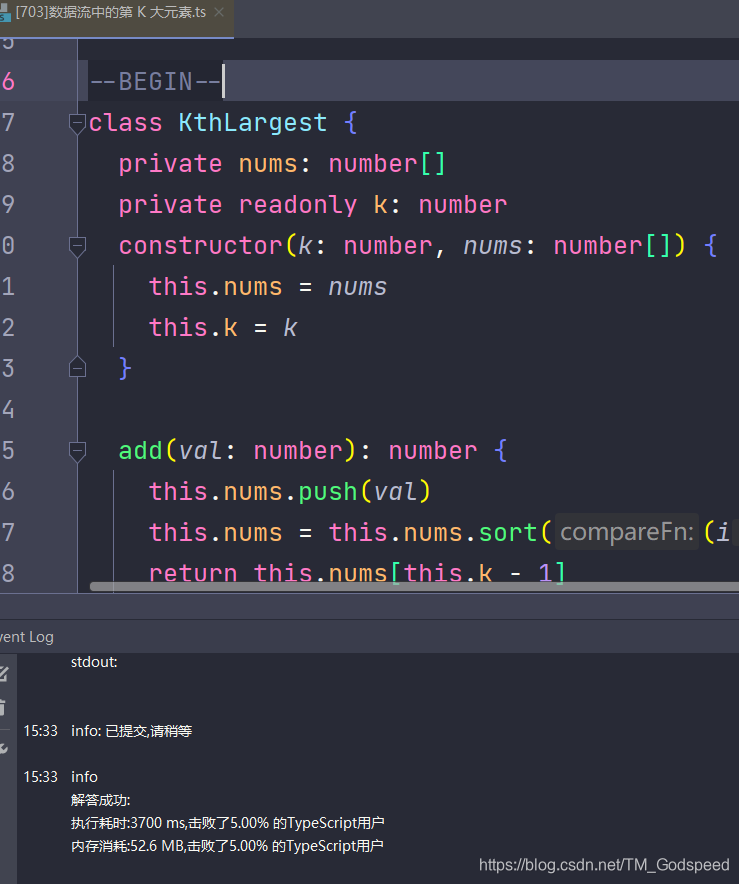
从提交结果来看原生的 sort() 在面对大量数据时表现出来的性能也一般，后面文章会介绍排序算法，希望大家能继续支持

leetCode 215 数组中的第k大元素

这道题可以用排序、大顶堆、小顶堆的方法解答

先介绍最简单的排序，使用排序的方法在函数中只要写1行代码即可

function findKthLargest(nums: number[], k: number): number {
  return nums.sort((i, j) => j - i)[k - 1]
}

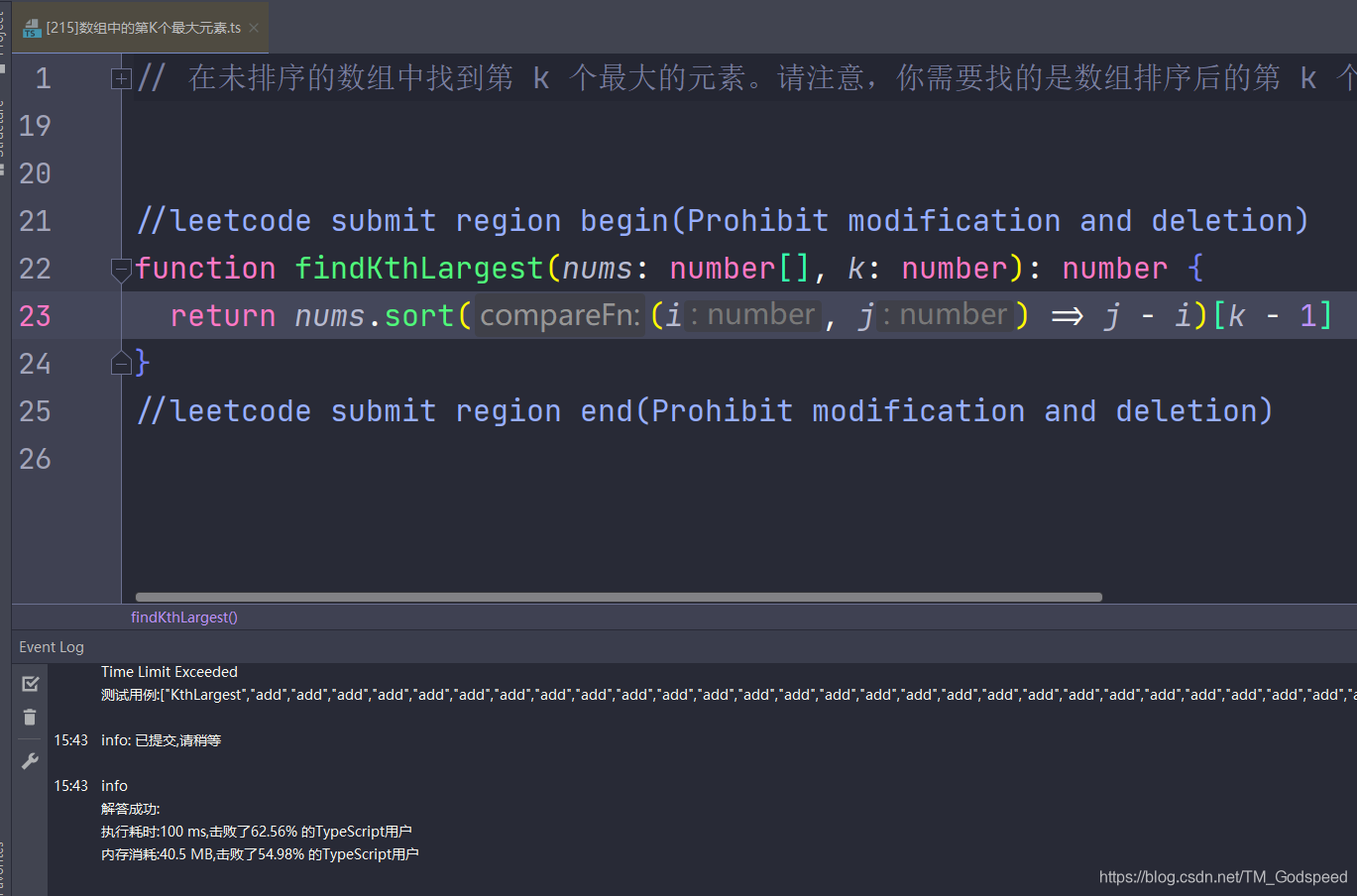
使用大顶堆的话只要弹 $k-1$ 次堆，最后堆顶元素即题目所求

class Heap {
  public data: number[]
  private readonly kind: boolean
  constructor(data: number[], kind: 'big' | 'small') {
    // 为了能用小顶堆解题而使用了深拷贝
    this.data = [...data]
    this.kind = kind === 'big'
    this.init()
  }
  
  private init() {
    for (let i = 1; i < this.data.length; i++) this.sortUp(i)
  }
  
  peek() {
    return this.data.length ? this.data[0] : null
  }
  
  size() {
    return this.data.length
  }
  
  push(val: number) {
    this.data.push(val)
    this.sortUp(this.data.length - 1)
  }
  
  pop() {
    if (!this.data.length) return null
    if (this.data.length === 1) return this.data.pop()
    const res = this.data[0]
    this.data[0] = this.data.pop()
    this.sortDown(0)
    return res
  }
  
  private sortUp(index: number) {
    let parentIndex: number
    while (index) {
      parentIndex = (index - 1) >> 1
      if (this.kind) {
        // 大顶堆
        if (this.data[index] > this.data[parentIndex]) this.swap(index, parentIndex)
        else break
      } else {
        // 小顶堆
        if (this.data[parentIndex] > this.data[index]) this.swap(index, parentIndex)
        else break
      }
      index = parentIndex
    }
  }
  
  private sortDown(index: number) {
    let leftIndex: number, rightIndex: number, target: number
    while (index < this.data.length) {
      leftIndex = (index << 1) + 1
      rightIndex = (index << 1) + 2
      target = index
      if (this.kind) {
        // 大顶堆
        if (leftIndex < this.data.length && this.data[leftIndex] > this.data[target]) target = leftIndex
        if (rightIndex < this.data.length && this.data[rightIndex] > this.data[target]) target = rightIndex
      } else {
        // 小顶堆
        if (leftIndex < this.data.length && this.data[leftIndex] < this.data[target]) target = leftIndex
        if (rightIndex < this.data.length && this.data[rightIndex] < this.data[target]) target = rightIndex
      }
      if (target === index) break
      this.swap(target, index)
      index = target
    }
  }
  
  private swap(i: number, j: number) {
    [this.data[i], this.data[j]] = [this.data[j], this.data[i]]
  }
}

function findKthLargest(nums: number[], k: number): number {
  const numsHeap = new Heap(nums, "big")
  for (let i = 0; i < k - 1; i++) {
    numsHeap.pop()
  }
  return numsHeap.peek()
}

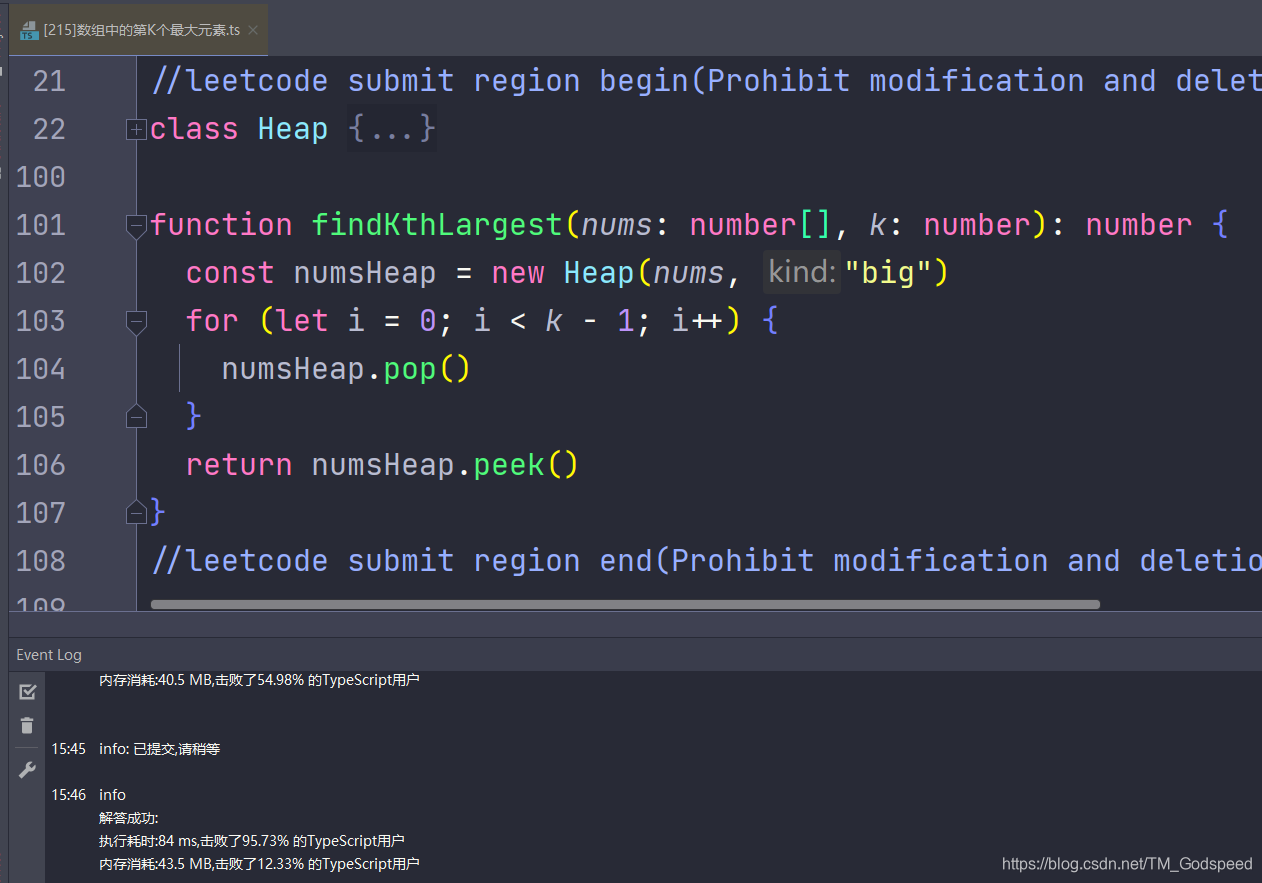
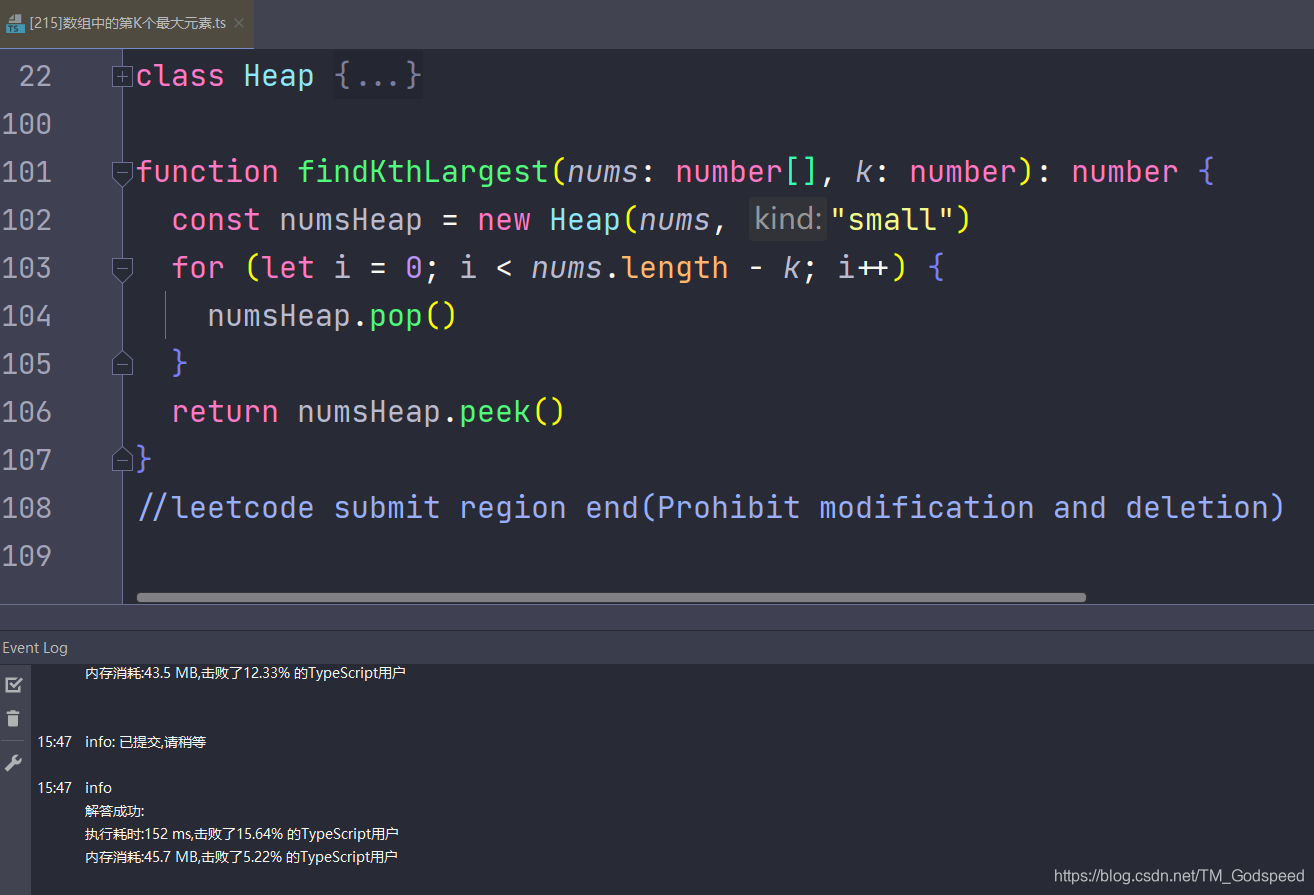
使用小顶堆的话只要弹 $length-k$ 次堆，最后返回堆顶即题目所求

class Heap {
  public data: number[]
  private readonly kind: boolean
  constructor(data: number[], kind: 'big' | 'small') {
    // 为了能用小顶堆解题而使用了深拷贝
    this.data = [...data]
    this.kind = kind === 'big'
    this.init()
  }
  
  private init() {
    for (let i = 1; i < this.data.length; i++) this.sortUp(i)
  }
  
  peek() {
    return this.data.length ? this.data[0] : null
  }
  
  size() {
    return this.data.length
  }
  
  push(val: number) {
    this.data.push(val)
    this.sortUp(this.data.length - 1)
  }
  
  pop() {
    if (!this.data.length) return null
    if (this.data.length === 1) return this.data.pop()
    const res = this.data[0]
    this.data[0] = this.data.pop()
    this.sortDown(0)
    return res
  }
  
  private sortUp(index: number) {
    let parentIndex: number
    while (index) {
      parentIndex = (index - 1) >> 1
      if (this.kind) {
        // 大顶堆
        if (this.data[index] > this.data[parentIndex]) this.swap(index, parentIndex)
        else break
      } else {
        // 小顶堆
        if (this.data[parentIndex] > this.data[index]) this.swap(index, parentIndex)
        else break
      }
      index = parentIndex
    }
  }
  
  private sortDown(index: number) {
    let leftIndex: number, rightIndex: number, target: number
    while (index < this.data.length) {
      leftIndex = (index << 1) + 1
      rightIndex = (index << 1) + 2
      target = index
      if (this.kind) {
        // 大顶堆
        if (leftIndex < this.data.length && this.data[leftIndex] > this.data[target]) target = leftIndex
        if (rightIndex < this.data.length && this.data[rightIndex] > this.data[target]) target = rightIndex
      } else {
        // 小顶堆
        if (leftIndex < this.data.length && this.data[leftIndex] < this.data[target]) target = leftIndex
        if (rightIndex < this.data.length && this.data[rightIndex] < this.data[target]) target = rightIndex
      }
      if (target === index) break
      this.swap(target, index)
      index = target
    }
  }
  
  private swap(i: number, j: number) {
    [this.data[i], this.data[j]] = [this.data[j], this.data[i]]
  }
}

function findKthLargest(nums: number[], k: number): number {
  const numsHeap = new Heap(nums, "small")
  for (let i = 0; i < nums.length - k; i++) {
    numsHeap.pop()
  }
  return numsHeap.peek()
}

leetCode 373 查找和最小的k对数字

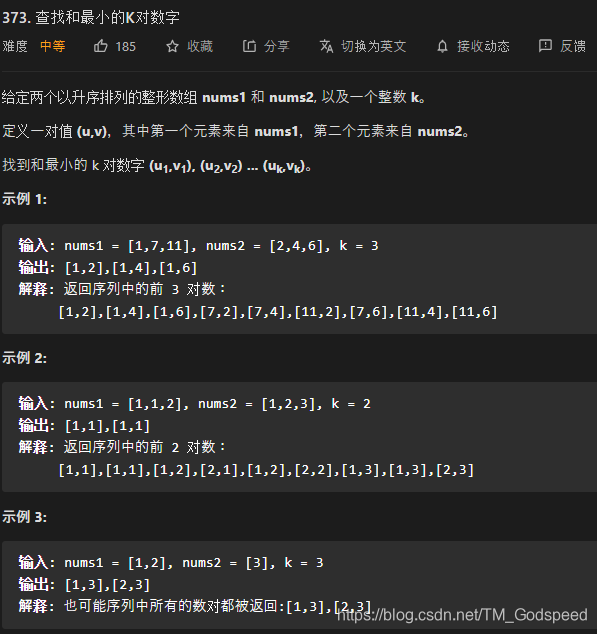
既然要找最小的元素，自然想到用小顶堆

当然本题不能像之前一样创建出来的堆的节点的数据类型是数字，在这里我定义节点的数据类型为 [[number, number], number]

第一个元素是一个数组，值为题目所提供的数字对；第二个元素是两个数字的和，进行上浮和下沉操作时比较的是节点的第二个元素

class SmallHeap {
  public data: [[number, number], number][]
  constructor(data: [[number, number], number][]) {
    this.data = data
  }
  
  private init() {
    for (let i = 1; i < this.data.length; i++) this.sortUp(i)
  }
  
  size() {
    return this.data.length
  }
  
  push(val: [[number, number], number]) {
    this.data.push(val)
    this.sortUp(this.data.length - 1)
  }
  
  pop() {
    if (!this.data.length) return null
    if (this.data.length === 1) return this.data.pop()
    const res = this.data[0]
    this.data[0] = this.data.pop()
    this.sortDown(0)
    return res
  }
  
  private sortUp(index: number) {
    let parentIndex: number
    while (index) {
      parentIndex = (index - 1) >> 1
      if (this.data[index][1] < this.data[parentIndex][1]) {
        this.swap(index, parentIndex)
        index = parentIndex
      } else break
    }
  }
  
  private sortDown(index: number) {
    let leftIndex: number, rightIndex: number, target: number
    while (index < this.data.length) {
      leftIndex = (index << 1) + 1
      rightIndex = (index << 1) + 2
      target = index
      if (leftIndex < this.data.length && this.data[leftIndex][1] < this.data[target][1]) target = leftIndex
      if (rightIndex < this.data.length && this.data[rightIndex][1] < this.data[target][1]) target = rightIndex
      if (target === index) break
      this.swap(index, target)
      index = target
    }
  }
  
  private swap(i: number, j: number) {
    [this.data[i], this.data[j]] = [this.data[j], this.data[i]]
  }
  
}

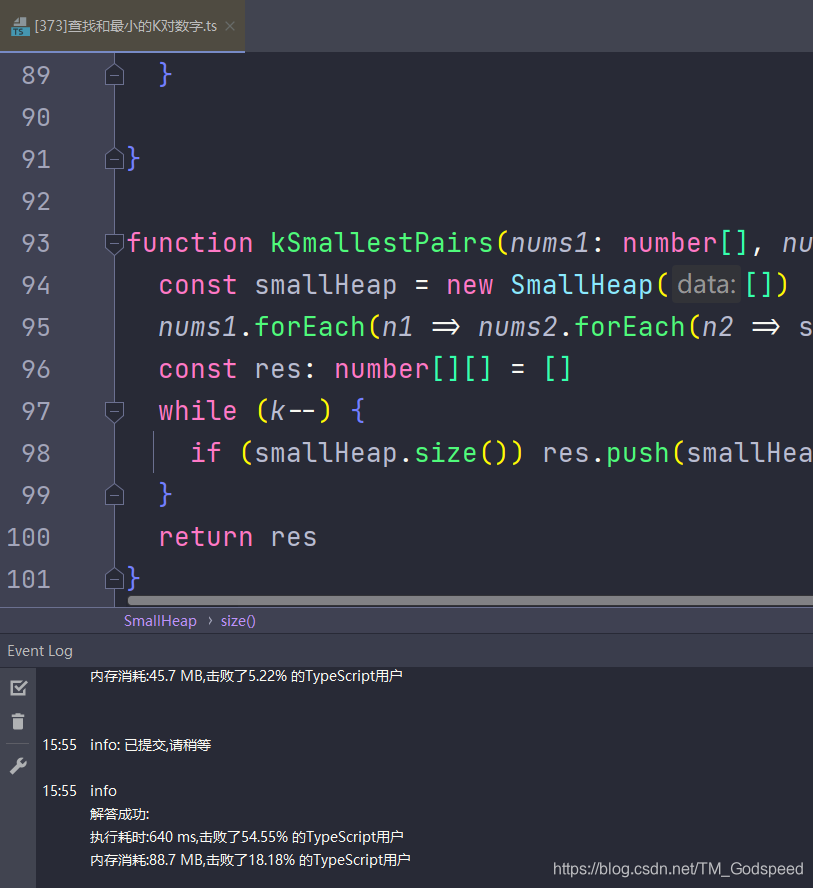
function kSmallestPairs(nums1: number[], nums2: number[], k: number): number[][] {
  const smallHeap = new SmallHeap([])
  nums1.forEach(n1 => nums2.forEach(n2 => smallHeap.push([[n1, n2], n1 + n2])))
  const res: number[][] = []
  while (k--) {
    if (smallHeap.size()) res.push(smallHeap.pop()[0])
  }
  return res
}

leetCode 692 前k个高频单词

这道题可以使用大顶堆来解题，堆中节点的数据类型为 [string, number]，第一个元素是单词，第二个单词是出现次数

这里的节点比较操作有两点，首先是比较出现次数，当出现次数相同时比较字符串，比较字符串的呃时候优先比较首字母的排序顺序，如果首字母相同则比较字符串长度，长度较小的优先

在 js 中字符串比较直接使用比较符号即可，其会按照上述规则进行比较

function topKFrequent(words: string[], k: number): string[] {
  const counter: { [key: string]: number } = {}
  const smallHeap: [string, number][] = []
  words.forEach(word => counter[word] = counter[word] ? ++counter[word] : 1)
  let i = 0
  for (let key in counter) {
    if (i < k) {
      smallHeap.push([key, counter[key]])
      if (i === k - 1) initHeap(counter, smallHeap, k)
    } else if (counter[key] > smallHeap[0][1] || (counter[key] === smallHeap[0][1] && key < smallHeap[0][0])) {
      smallHeap[0] = [key, counter[key]]
      sortDown(counter, smallHeap, k, 0)
    }
    i++
  }
  const temp = smallHeap.sort((a, b) => {
    if (a[1] > b[1]) return -1
    else if (a[1] < b[1]) return 1
    else {
      if (a[0] > b[0]) return 1
      else if (a[0] < b[0]) return -1
    }
  })
  return temp.map(item => item[0])
}

function initHeap(map: { [key: string]: number }, arr: [string, number][], len: number) {
  for (let i = len >> 1; i >= 0; i--) sortDown(map, arr, len, i)
}

function sortDown(map: { [key: string]: number }, arr: [string, number][], len: number, index: number) {
  const leftIndex = (index << 1) + 1, rightIndex = (index << 1) + 2
  let target = index
  
  if (leftIndex < len && (
    (map[arr[leftIndex][0]] < map[arr[target][0]]) ||
    ((map[arr[leftIndex][0]] === map[arr[target][0]]) && (arr[leftIndex][0] > arr[target][0]))
  )) {
    target = leftIndex
  }
  if (rightIndex < len && (
    (map[arr[rightIndex][0]] < map[arr[target][0]]) ||
    ((map[arr[rightIndex][0]] === map[arr[target][0]]) && (arr[rightIndex][0] > arr[target][0]))
  )) {
    target = rightIndex
  }
  if (target !== index) {
    swap(arr, target, index)
    sortDown(map, arr, len, target)
  }
}

function swap(arr: any[], i: number, j: number) {
  [arr[i], arr[j]] = [arr[j], arr[i]]
}

leetCode 295 数据流的中位数

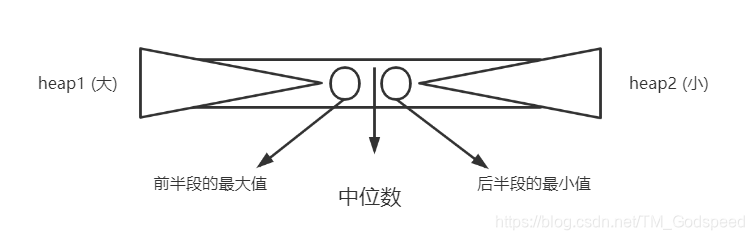
从上图可以发现，中位数的前一个数字是前半段的最大值，中位数的后一个数字是后半段的最小值，因此我们需要一个大顶堆维护前半段的数字，一个小顶堆维护后半段的数字

为了维护整个数列的有序性，在插入时我们需要以下规则

1. h1为空或者当前加入值≤h1堆顶时往h1里推，否则往h2里推
2. 使 $h1数量\ge h2数量+1$
3. 当h1和h2的数量和为奇数时，中位数就是h1堆顶;
   当h1和h2的数量和为偶数时，中位数就是两个堆顶和的平均值

class Heap {
  public data: number[]
  private readonly kind: boolean
  constructor(data: number[], kind: 'big' | 'small') {
    this.data = [...data]
    this.kind = kind === 'big'
    this.init()
  }
  
  private init () {
    for (let i = 1; i < this.data.length; i++) this.sortUp(i)
  }
  
  size() {
    return this.data.length
  }
  
  peek() {
    return this.data.length ? this.data[0] : null
  }
  
  push(val: number) {
    this.data.push(val)
    this.sortUp(this.data.length - 1)
  }
  
  pop() {
    if (!this.data.length) return null
    if (this.data.length === 1) return this.data.pop()
    const res = this.data[0]
    this.data[0] = this.data.pop()
    this.sortDown(0)
    return res
  }
  
  private sortUp(index: number) {
    let parentIndex: number
    while (index) {
      parentIndex = (index - 1) >> 1
      if (this.kind) {
        // 大顶堆
        if (this.data[index] > this.data[parentIndex]) this.swap(index, parentIndex)
        else break
      } else {
        // 小顶堆
        if (this.data[index] < this.data[parentIndex]) this.swap(index, parentIndex)
        else break
      }
      index = parentIndex
    }
  }
  
  private sortDown(index: number) {
    let leftIndex: number, rightIndex: number, target: number
    while (index < this.data.length) {
      leftIndex = (index << 1) + 1
      rightIndex = (index << 1) + 2
      target = index
      
      if (this.kind) {
        // 大顶堆
        if (leftIndex < this.data.length && this.data[leftIndex] > this.data[target]) target = leftIndex
        if (rightIndex < this.data.length && this.data[rightIndex] > this.data[target]) target = rightIndex
      } else {
        // 小顶堆
        if (leftIndex < this.data.length && this.data[leftIndex] < this.data[target]) target = leftIndex
        if (rightIndex < this.data.length && this.data[rightIndex] < this.data[target]) target = rightIndex
      }
      
      if (target === index) break
      this.swap(target, index)
      index = target
    }
  }
  
  private swap(i: number, j: number) {
    [this.data[i], this.data[j]] = [this.data[j], this.data[i]]
  }
}

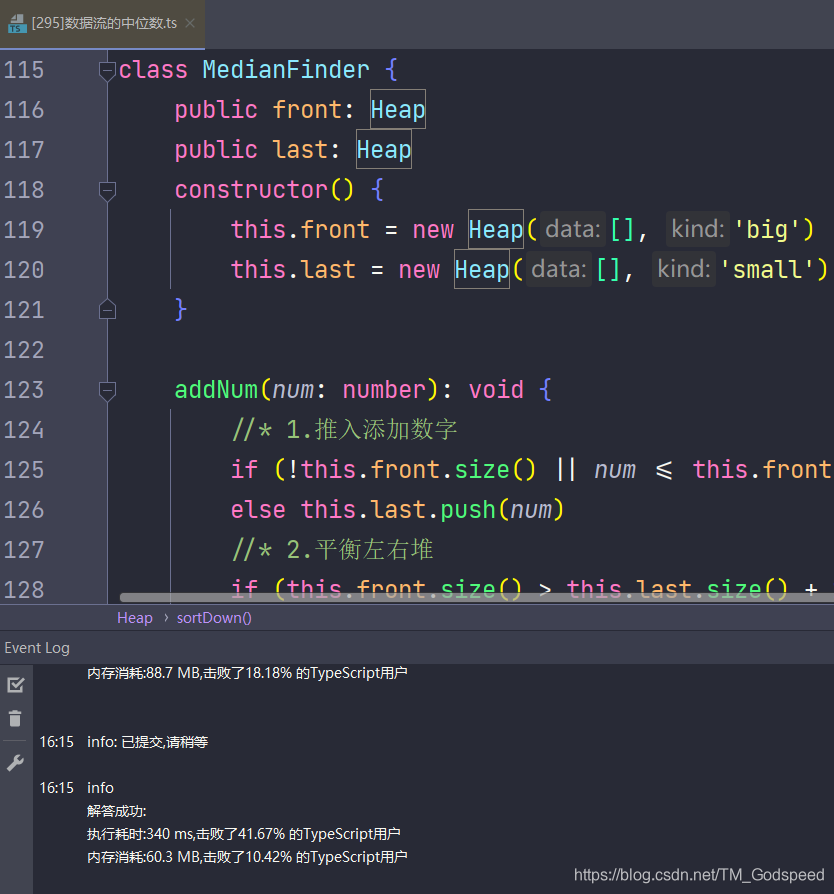
class MedianFinder {
  public front: Heap
  public last: Heap
  constructor() {
    this.front = new Heap([], 'big')
    this.last = new Heap([], 'small')
  }
  
  addNum(num: number): void {
    //* 1.推入添加数字
    if (!this.front.size() || num <= this.front.peek()) this.front.push(num)
    else this.last.push(num)
    //* 2.平衡左右堆
    if (this.front.size() > this.last.size() + 1) this.last.push(this.front.pop())
    if (this.last.size() > this.front.size()) this.front.push(this.last.pop())
  }
  
  findMedian(): number {
    const even = ((this.front.size() + this.last.size()) % 2) === 0
    if (even) {
      return (this.front.peek() + this.last.peek()) / 2
    }
    return this.front.peek()
  }
}

扩展
我们可以通过调整前后堆的数量关系维护数据流的任意位置，比如前三分之一后三分之一的位置

leetCode 1753 移除石子的最大得分

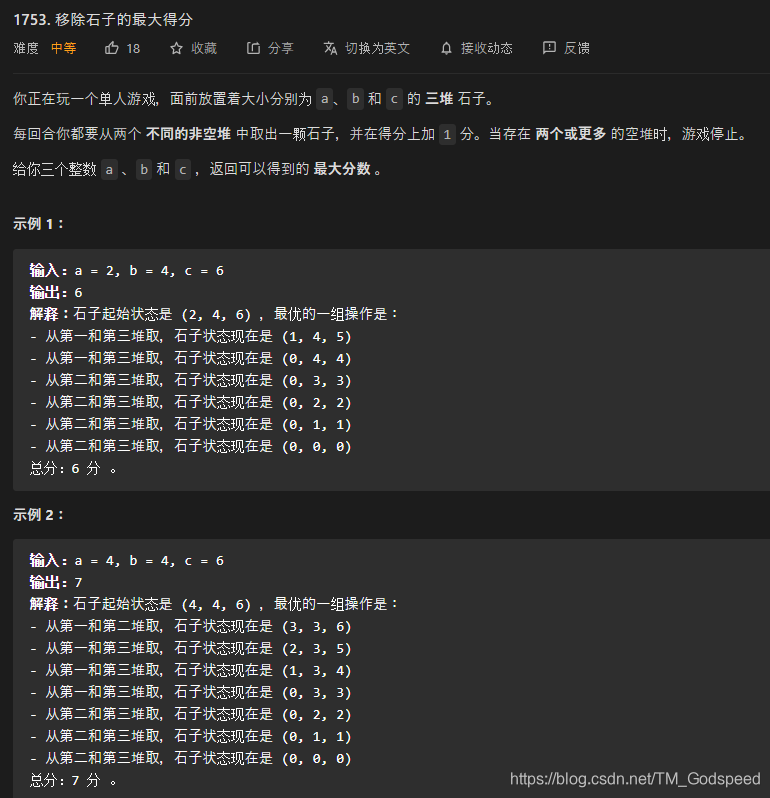
这道题其实就是一道脑筋急转弯的题目，这里给出的是一种解决方法，可能有其他解法

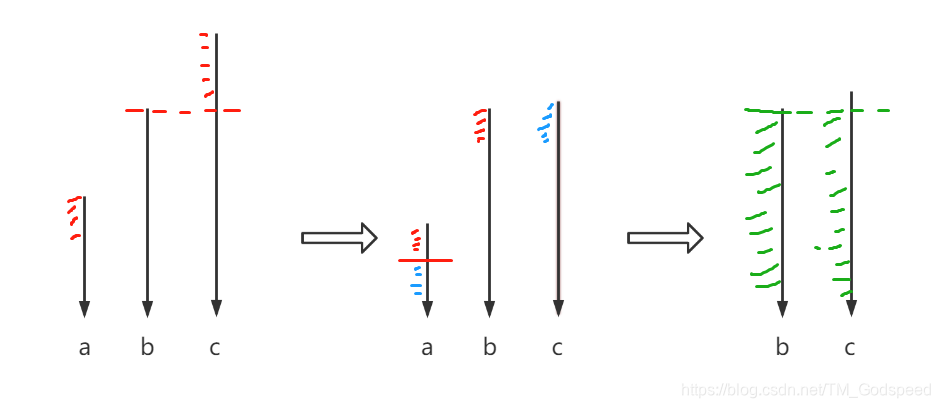
1. 首先给三个石堆排序为有序递增
2. 取c与b的差和a的最小值，得分增加该最小值，a减去该最小值(从逻辑上来看c也要减去该最小值，但是之后c就没用上，所以这里只要对a操作即可)
3. 当a为奇数时自减1使其变成偶数，b、c平分a，得分加a，b减去a的一半
4. 最后得分加b就是题目所求

上图并没有展示所有情况，但是所有情况经过上述步骤都能得到正解，读者想到其他情况的话可以套用上述步骤进行验证

function maximumScore(a: number, b: number, c: number): number {
  let ans = 0
  const sorted = [a, b, c].sort((a, b) => a - b)
  const min = Math.min(sorted[0], sorted[2] - sorted[1])
  ans += min
  sorted[0] -= min
  
  if (sorted[0] > 0) {
    if (sorted[0] % 2 === 1) sorted[0]--
    ans += sorted[0]
    sorted[1] -= sorted[0] / 2
  }
  
  return ans + sorted[1]
}

leetCode 1801 积压订单的订单总数

这道题的题目比较复杂，这里简单解释一下

题目会给出两种订单类型，购买订单和销售订单，在这两种订单中会给出价格和数量，最后我们要求出没有处理的订单总数

处理订单的原则只有一个：购买价格要≥销售价格 (不能赔本)

$利润=购买价格-销售价格$
为了使利益最大化，我们可以使用大顶堆来维护购买订单，使用小顶堆来维护销售订单

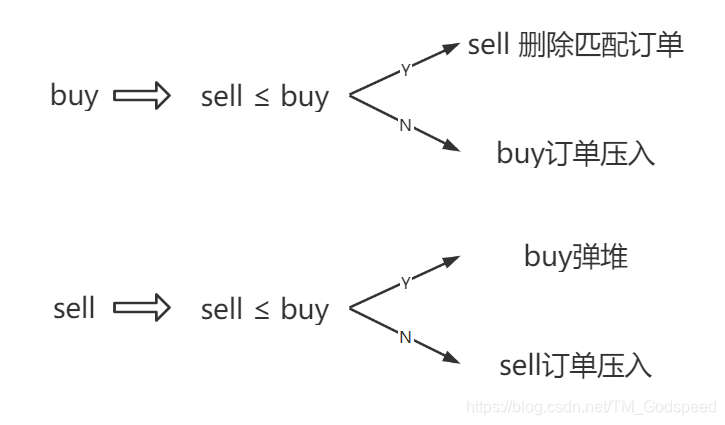
此题的堆的节点数据结构为 [number, number]，第一个元素表示价格，第二个元素表示订单数，在维护堆的时候比较的是价格

class Heap {
  // [价格, 订单数]
  public data: [number, number][]
  private readonly kind: boolean
  constructor(data: [number, number][], kind: 'big' | 'small') {
    this.data = data
    this.kind = kind === 'big'
    this.init()
  }
  private init() {
    for (let i = 1; i < this.data.length; i++) this.sortUp(i)
  }
  
  size() {
    return this.data.length
  }
  
  peek() {
    return this.data.length ? this.data[0] : null
  }
  
  push(val: [number, number]) {
    this.data.push(val)
    this.sortUp(this.data.length - 1)
  }
  
  pop() {
    if (!this.data.length) return null
    if (this.data.length === 1) return this.data.pop()
    const res = this.data[0]
    this.data[0] = this.data.pop()
    this.sortDown(0)
    return res
  }
  
  private sortUp(index: number) {
    let parentIndex: number
    while (index) {
      parentIndex = (index - 1) >> 1
      if (this.kind) {
        // 大顶堆
        if (this.data[index][0] > this.data[parentIndex][0]) this.swap(index, parentIndex)
        else break
      } else {
        // 小顶堆
        if (this.data[index][0] < this.data[parentIndex][0]) this.swap(index, parentIndex)
        else break
      }
      index = parentIndex
    }
  }
  
  private sortDown(index: number) {
    let leftIndex: number, rightIndex: number, target: number
    while (index < this.data.length) {
      leftIndex = (index << 1) + 1
      rightIndex = (index << 1) + 2
      target = index
      if (this.kind) {
        // 大顶堆
        if (leftIndex < this.data.length && this.data[leftIndex][0] > this.data[target][0]) target = leftIndex
        if (rightIndex < this.data.length && this.data[rightIndex][0] > this.data[target][0]) target = rightIndex
      } else {
        // 小顶堆
        if (leftIndex < this.data.length && this.data[leftIndex][0] < this.data[target][0]) target = leftIndex
        if (rightIndex < this.data.length && this.data[rightIndex][0] < this.data[target][0]) target = rightIndex
      }
      if (target === index) break
      this.swap(index, target)
      index = target
    }
  }
  
  private swap(i: number, j: number) {
    [this.data[i], this.data[j]] = [this.data[j], this.data[i]]
  }
}

function getNumberOfBacklogOrders(orders: number[][]): number {
  let res = 0, min = 0
  const buy = new Heap([], "big")
  const sell = new Heap([], 'small')
  
  // 0 buy  1 sell
  orders.forEach(([price, amount, orderType]) => {
    if (orderType) {
      // sell
      while (amount) {
        if (buy.size() && buy.peek()[0] >= price) {
          min = Math.min(buy.peek()[1], amount)
          buy.peek()[1] -= min
          amount -= min
          if (buy.peek()[1] === 0) buy.pop()
        } else {
          sell.push([price, amount])
          break
        }
      }
    } else {
      // buy
      while (amount) {
        if (sell.size() && price >= sell.peek()[0]) {
          min = Math.min(amount, sell.peek()[1])
          sell.peek()[1] -= min
          amount -= min
          if (sell.peek()[1] === 0) sell.pop()
        } else {
          buy.push([price, amount])
          break
        }
      }
    }
  })
  
  // 处理积压订单
  while (buy.size() && sell.size() && buy.peek()[0] >= sell.peek()[0]) {
    min = Math.min(buy.peek()[1], sell.peek()[1])
    buy.peek()[1] -= min
    sell.peek()[1] -= min
    if (!buy.peek()[1]) buy.pop()
    if (!sell.peek()[1]) sell.pop()
  }
  
  while (buy.size()) res += buy.pop()[1]
  while (sell.size()) res += sell.pop()[1]
  
  return res % 1000000007
}

leetCode 355 设计推特

这道题要注意的是我们要维护一个用户列表，这个用户列表维护的是每个用户的关注和自己发的推特，注意每个用户的关注中必须有自己(这样可以在获取推特的时候更方便处理)

由于测试用例只能一条一条执行，所以我们可以定义一个整形的数字来记录推特发表的时间

使用大顶堆来维护最新发表的10条推特，这个大顶堆的节点的数据结构为 [number, number]，第一个元素为推特id，第二个元素为推特发表时间，在维护堆的时候只要比较时间即可

class TweetsHeap {
    // [tweetId, time]
    public data: [number, number][]
    constructor() {
        this.data = []
    }
    
    size() {
        return this.data.length
    }
    
    push(val: [number, number]) {
        this.data.push(val)
        this.sortUp(this.data.length - 1)
    }
    
    pop() {
        if (!this.data.length) return null
        if (this.data.length === 1) return this.data.pop()
        const res = this.data[0]
        this.data[0] = this.data.pop()
        this.sortDown(0)
        return res
    }
    
    clear () {
        this.data = []
    }
    
    private sortUp(index: number) {
        let parentIndex: number
        while (index) {
            parentIndex = (index - 1) >> 1
            if (this.data[index][1] > this.data[parentIndex][1]) this.swap(index, parentIndex)
            else break
            index = parentIndex
        }
    }
    
    private sortDown(index: number) {
        let leftIndex: number, rightIndex: number, target: number
        while (index < this.data.length) {
            leftIndex = (index << 1) + 1
            rightIndex = (index << 1) + 2
            target = index
            if (leftIndex < this.data.length && this.data[leftIndex][1] > this.data[target][1]) target = leftIndex
            if (rightIndex < this.data.length && this.data[rightIndex][1] > this.data[target][1]) target = rightIndex
            if (target === index) break
            this.swap(index, target)
            index = target
        }
    }
    
    private swap(i: number, j: number) {
        [this.data[i], this.data[j]] = [this.data[j], this.data[i]]
    }
}

class Twitter {
    private time: number
    private users: {[key: number]: {followees: any, tweets: [number, number][]}}   // [tweetId, time]
    private tweetHeap: TweetsHeap
    constructor() {
        this.users = {}
        this.time = 0
        this.tweetHeap = new TweetsHeap()
    }

    postTweet(userId: number, tweetId: number): void {
        if (!this.users[userId]) this.users[userId] = {followees: new Set([userId]), tweets: []}
        this.users[userId].tweets.push([tweetId, this.time++])
    }

    getNewsFeed(userId: number): number[] {
        if (!this.users[userId]) this.users[userId] = {followees: new Set([userId]), tweets: []}
        this.users[userId].followees.forEach(followee => this.users[followee]?.tweets.forEach(t => this.tweetHeap.push(t)))
        const res: number[] = []
        while (this.tweetHeap.size() && res.length < 10) res.push(this.tweetHeap.pop()[0])
        this.tweetHeap.clear()
        return res
    }

    follow(followerId: number, followeeId: number): void {
        if (!this.users[followerId]) this.users[followerId] = {tweets: [], followees: new Set([followerId])}
        this.users[followerId].followees.add(followeeId)
    }

    unfollow(followerId: number, followeeId: number): void {
        this.users[followerId].followees.delete(followeeId)
    }
}

结语

这个系列会坚持更新，感谢支持

原文链接:https://blog.csdn.net/TM_Godspeed/article/details/117356454